Unit 4 test congruent triangles answer key – Welcome to the Unit 4 Test: Congruent Triangles Answer Key. This comprehensive resource provides a thorough review of the key concepts and theorems related to congruent triangles, equipping you with the knowledge and skills to excel in your geometry studies.
Throughout this guide, we will delve into the definitions, properties, and applications of congruent triangles, empowering you with a deep understanding of this fundamental geometric concept.
Congruent Triangles
Congruent triangles are two triangles that have the same shape and size. They have the same corresponding sides and angles.
Properties of Congruent Triangles
- Corresponding sides are equal in length.
- Corresponding angles are equal in measure.
- The triangles are superimposable, meaning they can be placed on top of each other to match exactly.
Examples of Congruent Triangles
Consider two equilateral triangles with side lengths of 5 cm. These triangles are congruent because all three sides and all three angles are equal.
Methods for Proving Triangle Congruence
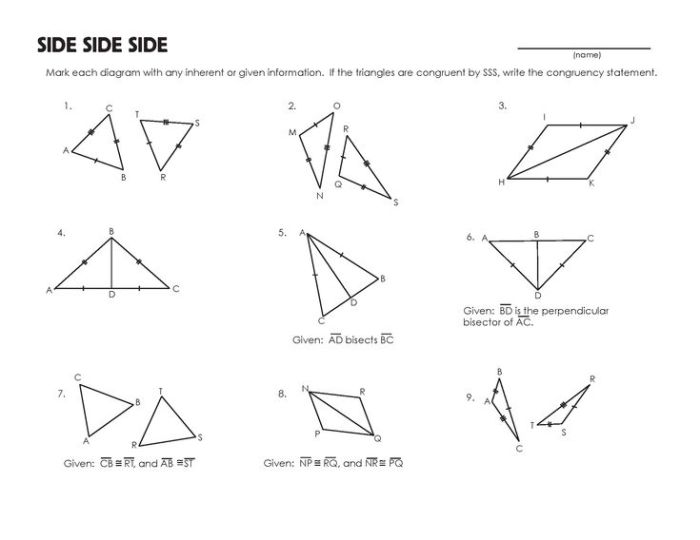
Side-Side-Side (SSS) Congruence Theorem
If the three sides of one triangle are congruent to the three sides of another triangle, then the triangles are congruent.
Side-Angle-Side (SAS) Congruence Theorem, Unit 4 test congruent triangles answer key
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
Angle-Side-Angle (ASA) Congruence Theorem
If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
Applications of Triangle Congruence: Unit 4 Test Congruent Triangles Answer Key
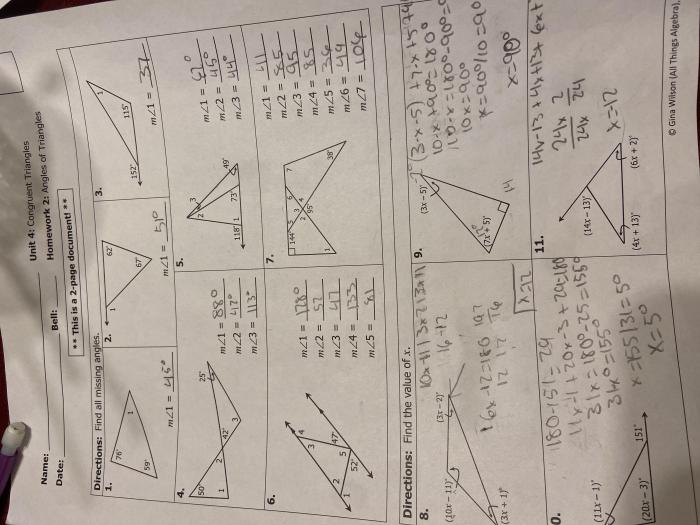
Geometry Proofs
Triangle congruence is used to prove many theorems in geometry. For example, it can be used to prove that the base angles of an isosceles triangle are congruent.
Real-World Scenarios
Triangle congruence is applied in many real-world scenarios, such as:
- Architecture: Designing buildings and structures that are symmetrical and balanced.
- Construction: Measuring and cutting materials to ensure accuracy and precision.
- Engineering: Designing bridges, airplanes, and other structures that require precise measurements.
Practice and Assessment
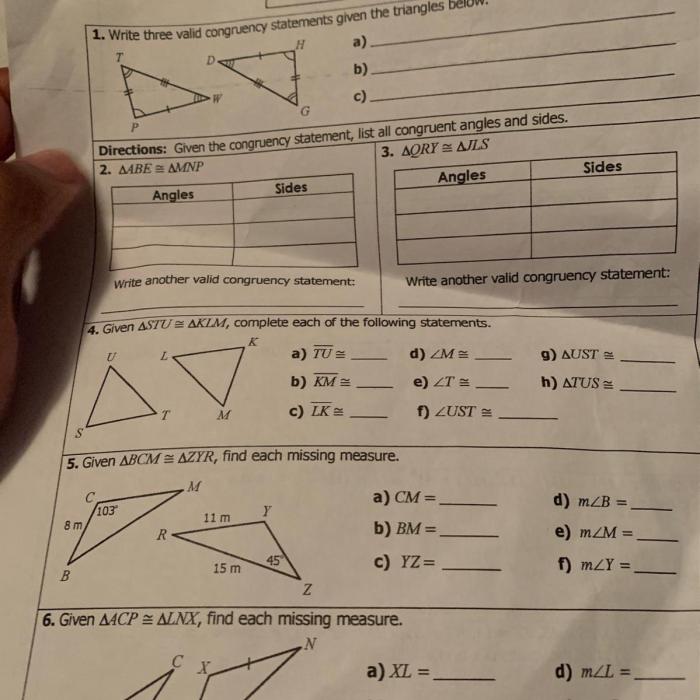
Practice Problems
| Problem | Solution |
|---|---|
| Prove that the triangles ABC and DEF are congruent given that AB = DE, BC = EF, and AC = DF. | Use the SSS Congruence Theorem. |
| Find the value of x if triangles GHI and JKL are congruent and GH = 10, HI = 12, and JK = 15. | Use the SAS Congruence Theorem. |
Practice Quiz
- Which of the following is a criterion for triangle congruence?
- State the ASA Congruence Theorem.
- Give an example of a real-world application of triangle congruence.
Step-by-Step Solutions
- SSS, SAS, ASA
- If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
- Designing symmetrical buildings or measuring materials for construction
FAQ
What is the definition of congruent triangles?
Congruent triangles are two triangles that have the same size and shape. This means that their corresponding sides and angles are equal.
What are the three congruence theorems?
The three congruence theorems are the Side-Side-Side (SSS) congruence theorem, the Side-Angle-Side (SAS) congruence theorem, and the Angle-Side-Angle (ASA) congruence theorem.
How can I use triangle congruence to solve geometry problems?
Triangle congruence can be used to solve a variety of geometry problems, such as finding missing side lengths, angles, or areas.